Lecture 02: Sampling and Fundamentals of Statistical Testing
Also check the Analysing Data Panopto page for recordings or the main Posit Cloud page for other materials.
Questions from the lecture
What does ‘moderated’ actually mean? I see it all the time in research papers and have an idea but i can’t really define it?
“Moderation” typically refers to a situation where the relationship between two variables changes when you account for a third variable. An “interaction” is a synonym and means the same.
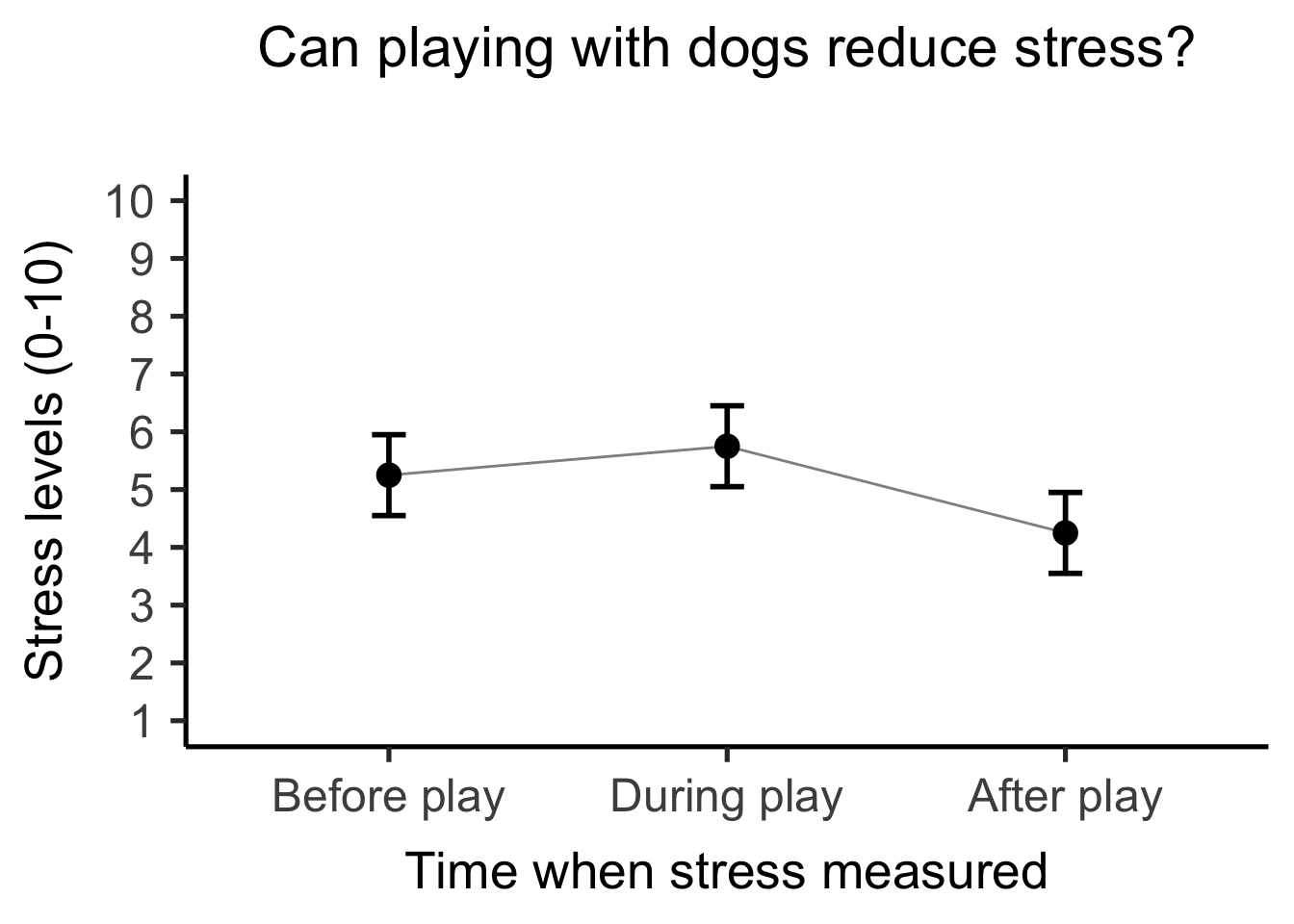
To use an example from last term, imagine you want to see whether playing with a dog reduces stress. You conduct an experiment where you measure participants’ stress before a play session, during and after. Here, you’re studying a relationship between two variables - stress levels and time (before vs during vs after). You might expect to see something like this:
But there’s a third variable that could be having impact - what if the participant doesn’t like dogs? Their experience of the play session would be very different. If we account for this variable, we could see something like this instead:
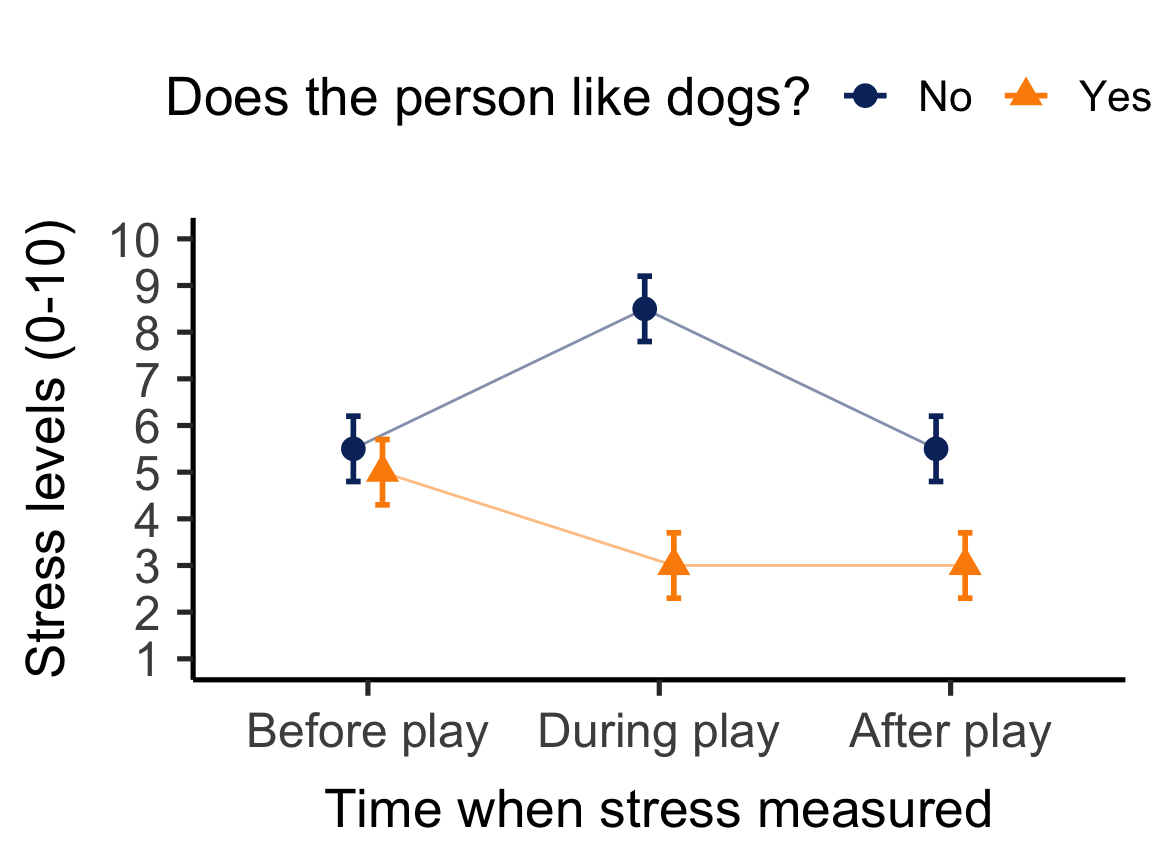
Therefore, the relationship between time point and stress level depends on whether or not the person likes dogs.
Do we need to remember the Forman and Leavens study?
Nope. We use examples from various fields of psychology because it’s more straightforward to explain statistical concepts in context rather than focusing on pure stats theory. I never expect you to remember details of the studies.
Is the example with Oreo the cat using z-score distribution or the proportions of scores used when talking about normal distribution? What does it mean by reverse the math to calculate a critical cut-off point for a specific probability?
When I say “reverse the math”, I mean that we have all the components needed to calculate this and we need to re-organise the equation. Consider the equation below (this is not directly relevant to the slides, but bear with me):
We know that:
\[X = Y + Z\]
Let’s say that we also know that X = 3, and Y = 1. We can reorganise the equation to calculate the value of Z:
\[3 = 1 + Z \] \[Z = 3-1\] \[Z = 2\]
In a similar way, we have these known values for Oreo:
- Oreo’s score X = 22.8
- Population mean M = 16.6
- Population SD = 4.7
At first, we wanted to find out the probability of obtaining Oreo’s score. Unfortunately for humanity, the equation for working out probability of a score in a normal distribution is this:
\[ f(x|\mu, \sigma^2) = \frac{1}{\sqrt{2\pi\sigma^2}} e^{-\frac{(x-\mu)^2}{2\sigma^2}} \ \]
I have no desire to manually work out the probability - labelled as \(f(x|\mu, \sigma^2)\) based on the equation above. So for the purposes of the demonstration, imagine the equation looks like this:
\[p = SD \times (X - M)\]
Where I’m using label \(p\) for probability instead. We know SD, X, and M, so we put them into the equation, which allows us to work out the probability:
\[p = 4.7 \times (22.8 - 16.6)\]
Now in the second example, we are interested in what Oreo’s score should be if he wanted to be in the top five 5% (which is equivalent to the probability of 0.05). So this time, we know the following values:
- p = 0.05
- Population mean M = 16.6
- Population SD = 4.7
We’re working with the same distribution, so the equation doesn’t change - we just know different components:
\[p = SD \times (X - M)\] \[0.05 = 4.7 \times (X - 16.6)\]
That’s what I mean by “reverse the math”. To reiterate, the simplified version of the equation is made up, but if we wanted to reverse it so we can calculate X, we could do the following:
First isolate the things in the parentheses:
\[\frac{0.05}{4.7} = X - 16.6 \]
Then isolate X:
\[X = \frac{0.05}{4.7} + 16.6 \]
And at that point you can complete the calculation.